Devlog 2 - Voronoi textures using roots of unity
Hi all, I’m back again…now we start with something fun today…generating better looking cells that seem truly random. Yeah sorry for getting straight into it…I’m dealing with a hearbreak right now, which is a story for another day, I will definitely put it out here on my blog. It’s just it has FINALLY COME TO AN END and I feel like I need some distraction, luckily I have this to work on. Also I QUIT MY JOB recently as it wasn’t working out… too much pressure and I don’t feel a personal connection with the team, as for the next steps idk…let’s see what time does…I feel like I need a break in my life right now, ever since college I never had a chance to breathe so this is good I guess, time to reflect and fix my life. So that’s what’s happening… soo many life updates… needs a separate blog post ufff… now shall we get to some nerdy math?.
Yes, today our goal is to generate the randomized phase offset cells for the voronoi textures using the same formula
\[f(x) = e^{i\theta}\]where \(\theta = (2\pi k) / N\), we try to add some randomness to \(\theta\) and see what it looks like shall we?
Lemma 2: Controlled Variation with Phase Offsets
Controlled variability in Voronoi cell form can be achieved by applying phase offsets to each root of unity, which makes the structure appear less regular while maintaining an underlying symmetry.
Proof: Without changing the overall circular distribution, each phase offset \(\theta_k\) modifies the final point position by slightly shifting the angle of the associated root of unity. We can provide the Voronoi cells controlled randomness by changing each \(\theta_k\) within a predetermined range.
Controlling variations
1. Phase variations
Phase varitions shifts the roots and generates polygons with irregular sides inside a circle of unit radius.
Take this python code:
import numpy as np
import matplotlib.pyplot as plt
def generate_randomized_polygon(n, offset_range=0.1, randomize=True):
"""
Generates a polygon based on the n-th roots of unity with optional random offsets.
Parameters:
n (int): Number of sides of the polygon.
offset_range (float): Maximum offset for randomizing the angle (radians).
randomize (bool): If True, randomize angles; otherwise, keep a perfect polygon.
Returns:
np.ndarray: x and y coordinates of the vertices.
"""
# Generate angles for n-th roots of unity
angles = np.linspace(0, 2 * np.pi, n, endpoint=False)
if randomize:
random_offsets = np.random.uniform(-offset_range, offset_range, n)
angles += random_offsets
# Calculate points using the exponential form: e^(i * theta)
points = np.exp(1j * angles)
x, y = points.real, points.imag
return x, y
# Parameters
n_sides = 5 # Number of sides for the polygon
offset = 0.6 # Range for randomizing angles
rows, cols = 2, 3 # Grid layout
# Create the plot
fig, axes = plt.subplots(rows, cols, figsize=(12, 8))
axes = axes.flatten()
# Plot the non-randomized polygon in the first subplot
x, y = generate_randomized_polygon(n_sides, offset_range=offset, randomize=False)
axes[0].fill(x, y, color='green', alpha=0.7, edgecolor='black', label='Non-Randomized')
axes[0].scatter(x, y, color='black') # Mark vertices
axes[0].set_aspect('equal', adjustable='box')
axes[0].set_title("Non-Randomized (Green)")
# Plot the randomized polygons in the other subplots
for i in range(1, len(axes)):
x, y = generate_randomized_polygon(n_sides, offset_range=offset, randomize=True)
axes[i].fill(x, y, color='yellow', alpha=0.7, edgecolor='black', label='Randomized')
axes[i].scatter(x, y, color='black') # Mark vertices
axes[i].set_aspect('equal', adjustable='box')
axes[i].set_title(f"Randomized Polygon {i}")
# Add a unit circle to all plots
for ax in axes:
unit_circle = plt.Circle((0, 0), 1, color='blue', fill=False, linestyle='--', linewidth=1)
ax.add_artist(unit_circle) # Add the unit circle to each subplot
# Fix all plots to the range [-1, 1] for both axes
for ax in axes:
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
# Adjust layout and show the plots
plt.tight_layout()
plt.show()
This will generate the output as below:
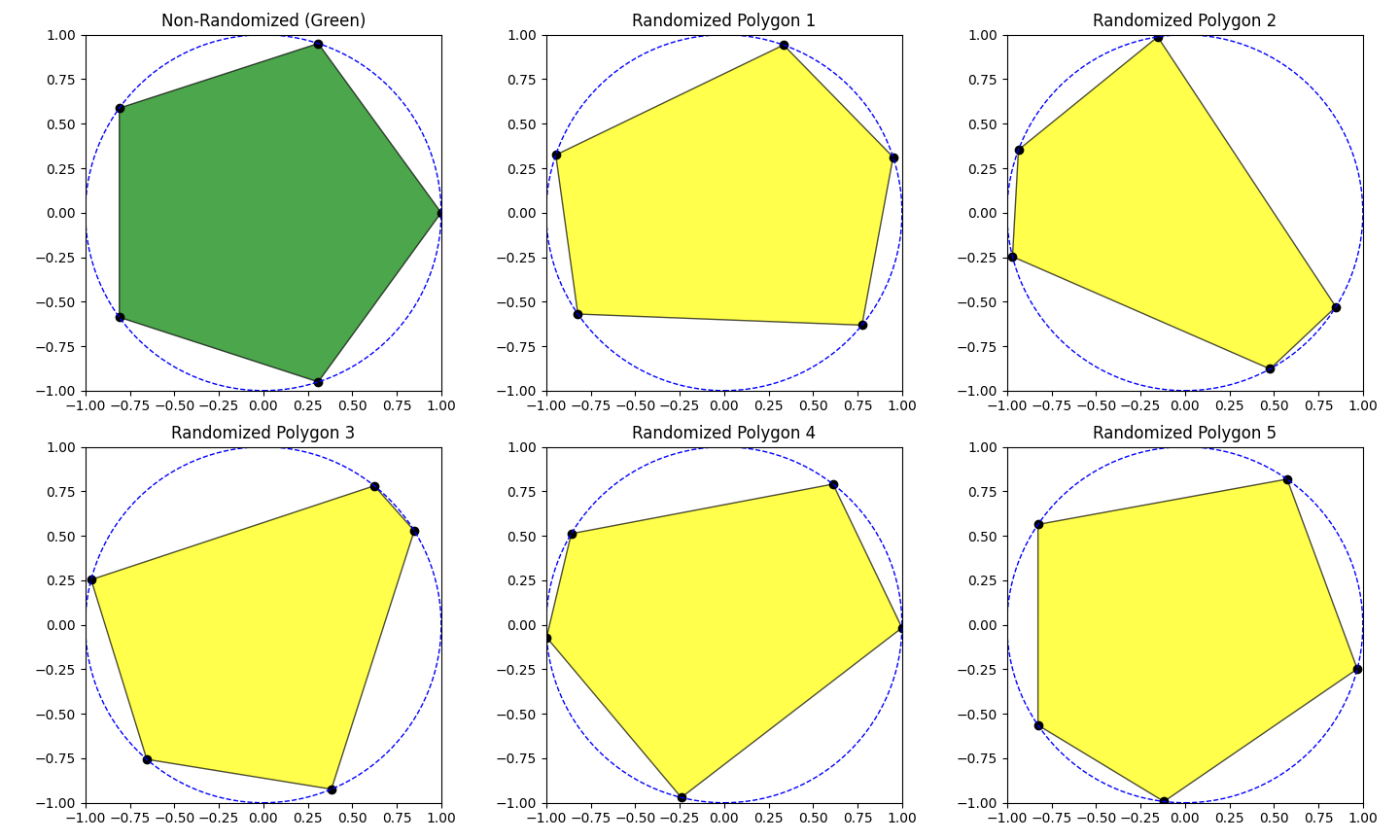
Next Goals
Now that we have introduced random offsets into the phase to shift the roots and create irregular polygons, we see how we can gain more control over it, ex. the cell size, side length. We try to parametrize the equation even further and analyze their variations.
Ending Thoughts
So to deal with life and hearbreaks here’s a song for y’all (been sampling indian inde scene recently and found this masterpiece by Nanku.)
https://music.apple.com/in/album/itti-si/1778176028?i=1778176030
I hope you like this song. To life 🥂
See you soon.